Principle of Superposition of Waves

Equation of resultant wave on string after interference :-

(iii) Two waves ${\mathrm{y}}_1=8\sin \left(\mathrm{wt}-\frac{\mathrm{\pi }}{2}\right)$ and ${\mathrm{y}}_2=6\sin \left(\mathrm{wt}-\frac{\mathrm{\pi }}{2}\right)$ are interfering one another. What will be the resultant amplitude.

Equation of resultant wave on string after interference :-

Equation of resultant wave on string after interference :-

(i) The amplitude of two interfering waves are $2a \& 3a$ respectively. The resultant amplitude in case if consructive interference.

Draw the graph of destructive interference pattern on string.

What is constructive interference on string?

An organ pipe open at both ends produces:

The disturbances produced by two sound sources cannot be cancelled as the disturbance by each wave is added.

What do you understand by principle of superposition of waves?

The maximum intensity of fringes in Young's experiment is $I$. If one of the slit is closed then, the intensity at that place becomes $I_o$. Which of the following relations is true? 

Three waves of equal frequencies having amplitudes $10 \mathrm{\mu m}, 4 \mathrm{\mu m}$ and $7 \mathrm{\mu }\mathrm{m}$ arrive at a given point with successive phase difference of $\frac{\pi }{2}.$ The amplitude of the resulting wave in $\mathrm{\mu }\mathrm{m}$ is given by, 

Two waves are passing through a region in the same direction at the same time. If the equation of these wave are

$y_1=a\sin \frac{2\pi }{\lambda }\left(vt-x\right)$

$y_2=b\sin \frac{2\pi }{\lambda }\left[\left(vt-x\right)+x_0\right]$,

then the amplitude of the resultant wave for $x_0=\frac{\lambda }{2}$ is,

The equations of two interfering waves on the string are given below:

$y_1=A\sin k\left(x-vt\right)$

$y_2=A\sin k\left(x-vt+x_o\right)$

Where $k=3.14 {\mathrm{cm}}^{-1}$, $x_o=3 \mathrm{cm}$, $A=2 \mathrm{cm}$. Find the amplitude of the resultant wave.

State and explain the principle of superposition of waves.

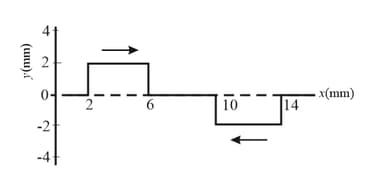
Figure shows two wave pulses at $t=0$ travelling on a string in opposite directions with the same wave speed $50 \mathrm{cm} {\mathrm{s}}^{-1}$. Point the values on graph for the string at $\mathrm{t}=4 \mathrm{ms}, 6 \mathrm{ms}, 8 \mathrm{ms},$ and $12 \mathrm{ms}$.

Matter waves after leaving the source, spread out in all the directions.

Two-point sources separated by $2.0 \mathrm{m}$ are radiating in phase with $\lambda =0.50 \mathrm{m}$. A detector moves in a circular path around the two sources in a plane containing them. How many maxima are detected?

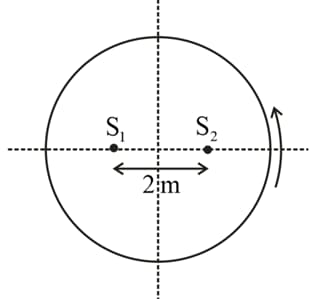
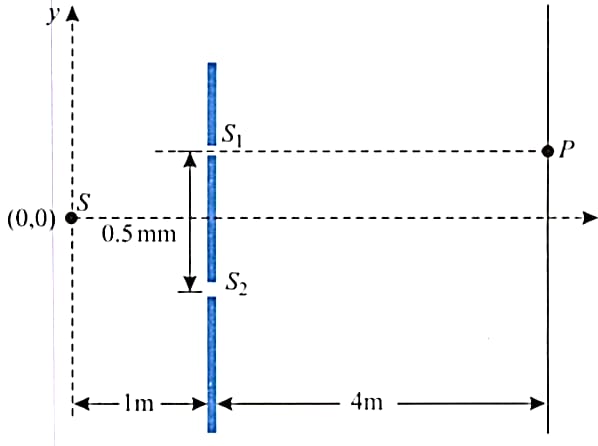
Figure shows a Young’s double slit experiment setup. The source $S$ of wavelength $4000Å$ oscillates along $y-$ axis according to the equation $y=\sin \pi t$, where $y$ is in millimeters and $t$ is in seconds. The distance between two slits $S_1$ and $S_2$ is $0.5\mathrm{m}\mathrm{m}$.

In Young's double slit experiment, the intensity of light coming from one of the slits is double the intensity from the other slit. The ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed is

Two waves are described by the equations:

${\mathrm{y}}_1=\mathrm{A}\cos \left(0.5\mathrm{ }\mathrm{\pi }\mathrm{x}-100\mathrm{\pi }\mathrm{t}\right)$

And ${\mathrm{y}}_2=\mathrm{A}\cos \left(0.46\mathrm{ }\mathrm{\pi }\mathrm{x}-92\mathrm{\pi }\mathrm{t}\right)$

Here x and y are in m and t is in s.



The number of maximum heard in one second will be

Intensity and phase of three sound wave reaching at some point in space is ${\mathrm{I}}_0,\mathrm{ }4\mathrm{ }{\mathrm{I}}_0,\mathrm{ }{\mathrm{I}}_0$ and ${10}^{\mathrm{o}},\mathrm{ }{130}^{\mathrm{o}}$ and ${250}^{\mathrm{o}}$ respectively. Resultant intensity at that point will be -